Uniform Distribution exercice 2

Let’s say x is uniformly distributed with beginning a = 20 and ending b = 40, Now solve the below questions.

1. Calculate P(x>30)
2. Calculate P(30<x<80)
3. Calculate P(0<x<10)

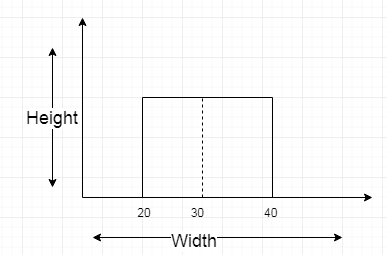
We already seen how to calculate height and width(Qbase) in our previous post.If the draw a uniform distribution for the given parameters this how it looks like

Calculate P(x>30)

We need to find the probability of x is greater than 30 from the below normal distribution.

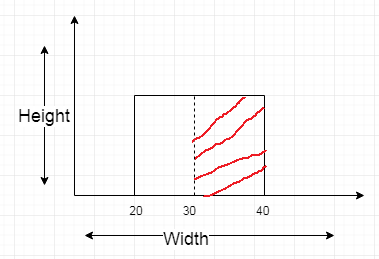
P(x>30) = width * height

Calculate Height:

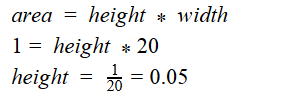
Calculate Width:

     in our case we need to find the width between 40 and 30 as we need to find P(x>30)

        So P(x>30) = 10*0.05= 0.5

So chances of  P(x>30) is with 50% probability.

Calculate P(30<x<80)

        In our case a= 20 and b= 40, means we don’t have 80 and we already calculate P(x>30)..

        As we know P(x>30) will be equal to P(30<x) or P(x<30), because 30 will be in between 20 and 40 there will be equal chances of P(x>30) and P(x<30)

        So P(30<x<80) will be 50% chances.

Calculate P(0<x<10):

        Simple the probability of P(0<x<10) will be zero as we have parameters between 20 and 40.