Uniform Distribution

A uniform distribution, sometimes also known as a rectangular distribution, is a distribution that has constant probability.

It is defined by two parameters a and b where a is minimum and b is maximum

Lets solve the below  problem.

        What is the probability of x >20 (P(x>20)) and x will be uniform distributed with parameters a=10 and b=30  (x~uniform(10,35))

        When we draw a uniform distribution, it looks like below.

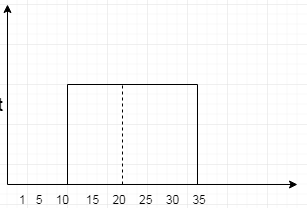
To solve the question we need to know two things one is question base/width,height, mean and variance.first let’s understand this and then we will solve our problem.

 1)Let’s find out mean and variance for one of our question  x~ uniform(10,35).

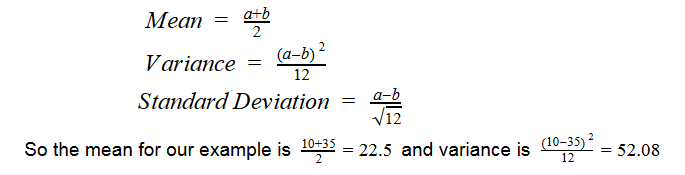
2) Now we will find height and width of our below uniform distribution

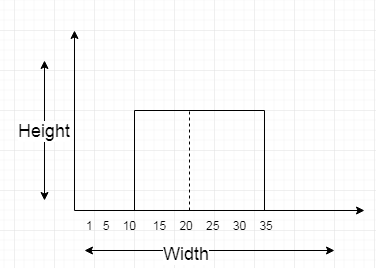
To find the  height of the distribution. The area under a probability distribution is always 1. As there are 35 units (from 10 to 35), then the height is 1/25.

Lets calculate height;        

As per the above definition area will be 1.

Q) P(x>20)

        p(x>20) = width * height

               For height we took 35-10 because we need to find the probability in between this

               For width we took 35-20, because we need to find the probability p(x>20) means between 20 and our b values 35

 When we substitute above values.

        p(x>20) = 15*0.04 = 0.6

So it is 0.6 or 60 percent probability that p(x) will be greater than 20